Kronecker積によるパラメータ削減

Kento Nozawa
10 May 2018

博士課程に入って36ヶ月の1ヶ月が過ぎてビビっています。

これを使って重み行列を小さくできると思ったのですが、調べたら既にあったのでブログ成仏です。

導入

Kronecker積（以下kron）という行列演算があります。Graph MLだと、JureさんのKronecker graphやその派生系で使われてたりします。そこで知りました。Wikipediaの記事によるとスパコンのベンチマークの Graph500 でKronecker graphが使われているそうです。

例えば \(A, B \in \mathbb{R}^{2 \times 2}\) という行列に対するkronは、以下のようになります。

\[A \otimes B = \begin{bmatrix} A_{11}B_{11} & A_{11}B_{12} & A_{12}B_{11} & A_{12}B_{12} \\ A_{11}B_{21} & A_{11}B_{22} & A_{12}B_{21} & A_{12}B_{22} \\ A_{21}B_{11} & A_{21}B_{12} & A_{22}B_{11} & A_{22}B_{12} \\ A_{21}B_{21} & A_{21}B_{22} & A_{22}B_{21} & A_{22}B_{22} \\ \end{bmatrix}\]

kronで生成される行列は、元の2つの行列の行数、列数をそれぞれ\((r_0, c_0), (r_1, c_1)\)とすれば、行数が\(r_0*r_1\)で、列数が \(c_0*c_1\) になります。このため、kronの演算回数に対して指数的に大きな行列が作れます。例えば、 \(A \in \mathbb{R}^{2 \times 2}\) に同じ次元をもつ \(X \in \mathbb{R}^{2 \times 2}\) を使って10回kronを行えば、\(2048 \times 2048\)の行列が構成できます。仮に\(A=X\)とすれば、パラメータ4つからこのような大きな行列が構成できることになります。

さて、ある日、kronを使えばニューラルネットのパラメータを減らせるなという気持ちに至ります。とりあえず全結合層のニューラルネットで実験してみました。

ネットワーク構成

MNISTを3層のMLPで分類します。構成はこんな感じにしました：

Input: 784ユニット
Hidden 625ユニット relu
Output 10ユニット softmax

重み行列のパラメータ数だけを考えると、

Input--Hidden で 490000
Hidden--Output で 6250

で合計 496250 のパラメータが必要です。 Pytorchで定義するとこんな感じです。

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(28*28, 625)
        self.fc2 = nn.Linear(625, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return F.log_softmax(x, dim=1)

次にkronを使うことを考えます。まず大きいのは Input--Hiddenです。 \(U, V \in \mathbb{R}^{28 \times25}\) という2つ行列にkronを使えば、同じサイズの重み行列が作れます。このとき、Input--Hiddenの重み行列のパラメータ数はもとが490000に対して2x28x25=1400です。

更に減らしてみましょう。先程の行列を \(U=V\) にできます。これでパラメータ数は 700 になりました。行数と列数は素因数分解できるのでもっと減らせますが、とりあえずこのくらいにします。

次に Hidden--Ouputです。 \(W \in \mathbb{R}^{10 \times 625}\)だったのを \(U \in \mathbb{R}^{5 \times 25}, V \in\mathbb{R}^{2 \times 25}\) にできます。先ほど違って10のrootが整数ではないので次元数が異なります。このとき、Input--Hiddenの重み行列のパラメータ数はもとが6250に対して5x25+2x25=175です。

以上のパターンとパラメータ数をまとめます。

名称	パラメータ数	説明
Original	\(496\,250\)	ナイーヴなニューラルネット
one-kron-mat	\(6\,950\)	`Input--Hidden` だけkron、分解した行列は同一
two-kron-mat	\(7\,650\)	`Input--Hidden` だけkron
one-kron-mat out-kron	\(875\)	2つのレイヤーでkron、`Input--Hidden`で分解した行列は同一
two-kron-mat out-kron	\(1\,575\)	2つのレイヤーでkron

実験

PyTorch examplesのMNISTと同じ設定です。epochは35回としました。

結果

acc loss

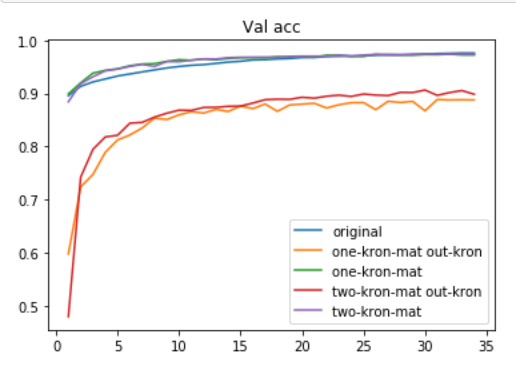
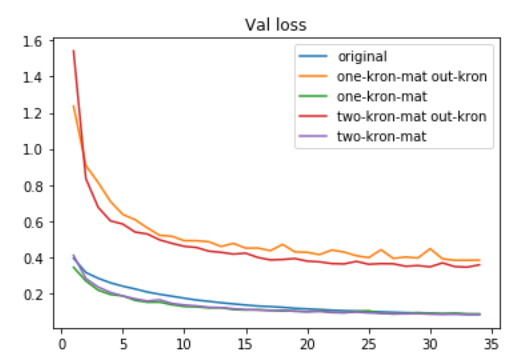
Input--Hiddenだけをkronで構成しても性能が落ちない
Input--Hiddenのkronに使う行列を同一としても性能が落ちない
Hidden--Outputをkronで構成するとけっこう負ける

ちなみにkronで構成するパラメータと同じ数のパラメータ数をもつナイーヴなニューラルネットの場合，中間層の次元数は10くらいになり、ここまで性能は出ません。

おわりに

検索したらそれらしい研究が既にありました。

この他のニューラルネットでの使われ方としてnatural gradientの近似に使う方法もICMLやICLRで出ています。

謝辞

議論に付き合っていただいたhimkt氏に感謝です。